算法题练习笔记

本文最后更新于：8 个月前

牛客上做算法练习时记录的思路，以及一些知识点、或者技巧，方便日后快速回顾

一、链表

题单：模板速刷TOP101

题目 描述
BM1 反转链表 反转整个链表，错误教训：当链头变为链尾时，一定要将链头的next指向NULL
BM2 链表内指定区间反转 巧妙利用“前哨”节点，让链头永远不变，避免分情况讨论的麻烦。巧妙利用一个temp指针，在区间内转换指针方向
BM3 链表中的节点每k个一组翻转 BM2的反转方法巧妙高效，但不适用于这题，因为它的使用建立在反转区间在链表长度范围内的条件上。但是这题要求，最后长度不足k的区间，保持原样。所以这就要求需要先遍历链表，获取到长度为k的区间进行反转，长度不足k的区间不做改动。
合并两个排序的链表 “前哨”，递归做法和迭代做法
合并k个已排序的链表 递归分治，优先队列两种做法
BM6 判断链表中是否有环 快慢指针，如果链表有环，那么环一定出现在链尾，也就意味着链表没有NULL，只要设置一快一满两个指针，就一定会相遇（快的每次走两步，满的每次走一步）
BM7 链表中环的入口结点 BM6的进阶，首先判断链表是否有环。如果有环，首先了解一个特点，快指针走的步数是慢指针的两倍。
假设链头到环入口的距离为x，环入口距离相遇点的距离为y，相遇点向后到环入口的距离为z，
且假设快指针在环里转了a圈，慢指针在环里转了b圈。那么就有 x+y+a(y+z) = 2[x+y+b(y+z)]，
整理一下得到：(a-2b)(y+z)=x+y，代表的含义是：从相遇点出发，一个指针在环里转若干圈，
另一个指针从头开始，最终会在原来的相遇点再次相遇；那么在相遇之前，从环入口到相遇点这段路程两个指针是重叠的，由此可以得出两个指针第一个重叠的地方就是环入口。
BM8 链表中倒数最后k个结点 双指针，前后指针，间隔k步
BM9 删除链表的倒数第n个节点 双指针，前后指针，“前哨”结点是处理很多链表问题的很好的技巧
BM10 两个链表的第一个公共结点 双指针，获取链表长度，长的先走，让两条链距离公共点的起点相同
BM11 链表相加(二) 反转链表 + 模拟加法 + 反转链表
BM12 单链表的排序 BM4合并两个有序链表，链表的归并排序，左边界是链表起点，右边界是NULL
递归三要素：终止条件、返回值、本级任务
BM13 判断一个链表是否为回文结构 抓住关键：前序和后序一致即为回文，可以用头插法new一个逆序链表，可以用栈，可以保存到数组中用前后对撞指针
BM14 链表的奇偶重排 一共就两种情况，奇数个节点或者偶数个节点，只要把两种情况的处理方式综合考虑进来，理清逻辑，就很容易解决了。
BM15 删除有序链表中重复的元素-I 前后指针pre和cur
BM16 删除有序链表中重复的元素-II 与BM15相比，难度提升在于，BM15保留了一个重复元素，而这里要把所有都删除，所以需要增加一个指针记录重复元素前一位的元素，用了三个指针pre、cur和nex，函数体里面分为两部分，一个是删除部分，与之对立的是指针前进部分
拓展：如果链表是无序的，则使用哈希表map，统计每个节点值出现的次数

小结

  • 链表主要考察点有：一、对链表指针的修改，如反转、删除、合并、分离等等。二、对链表性质的考察，如判断链表是否有环、寻找链表环入口、寻找链表之间的公共节点等等。
  • 链表题中常用的技巧有：双指针、前哨节点
  • 双指针，又可以分为：快慢指针、前后指针、两条链各一个指针。指针的方向可以是同向间隔k步，同向速度不同、反向
  • 前哨节点，涉及到链头可能变动时，增加前哨节点可以减少讨论的情况

二、二分查找/排序

牛客TOP101

题目 描述
BM17 二分查找-I
BM18 二维数组中的查找 一开始注意到了：左上角最小、右下角最大的规律，但是思路陷入了误区，以为要想BM17一样不断通过二分划分新的象限区间，在新的象限里面进行寻找（这样做，坐标计算非常棘手）。
但是没有注意到：上方 < 左下角 < 右方 这个特点，利用这个特点，加上以左下角为起点，可以实现
二分查找，如果target比当前大，就往右平移；如果target比当前小，就往上平移。结束条件是越过上或右边界
BM19 寻找峰值 利用二分，找波峰。二分向左还是向右的判断条件是mid和mid+1的大小比较
BM20 数组中的逆序对 归并排序统计法，归并排序分为（递归）划分和合并两个步骤，在向上合并的过程中，如果右数组元素比左数组剩余元素小，那么左数组剩余的元素个数就是逆序对的数量。在合并的过程中不断把这个数量累加起来，就得到最终结果
BM21 旋转数组的最小数字 旋转数组在旋转前可以视为AB两段，旋转后为BA（A可能为空数组）。那么在B段和A段中，元素都是升序的
取数组中点元素，如果中点 > 右边界，说明中点处于B段，此时最小值在A段，左边界向右移动 L = mid+1
如果中点 < 右边界，说明此时中点处于A段，最小值可能在中点左边，也可能中点就是最小值，所以右边界左移但包含中点，R=mid
如果中点 = 右边界， 此时中点既可能在A段、也可能在B段，所以需要让右边界左移，继续观察
BM22 比较版本号 这题算到二分有点牵强，唯一的“二”体现在用了双指针，就是两个字符串各一个索引指针。
通过将.与.之间的字符串转换为数字进行比较
  • 二分判断的条件有：指定target值与mid值比较、mid值与相邻的mid+1值比较、mid值与right值比较

三、二叉树

题目 描述
BM23 二叉树的前序遍历 递归思路（简单）：终止条件：指针为空，返回值：无，本级任务：取值加入数组、遍历左子树、遍历右子树。
非递归思路（栈）
BM24 二叉树的中序遍历 递归思路（简单）
非递归（栈），比前序麻烦，做的不对会陷入“重复进入子树”的困境
BM25 二叉树的后序遍历 递归思路（简单）
非递归（栈），比中序麻烦，需要判断右子树有没有被访问过才能决定是否读取根
BM26 求二叉树的层序遍历 方法一：借助队列，两层循环，外循环遍历树的层；内循环遍历当前层的所有节点。
利用queue.size()来获知当前层节点的个数，然后通过for循环遍历
方法二：递归，可以利用前中后序任意一种遍历，在递归遍历时增加一个参数记录当前深度，然后将节点加到对应深度所在的vector中，需要特别注意vector<vector> 的初始化
BM27 按之字形顺序打印二叉树 与BM26一样的思路，增加一个间隔逆序的操作
BM28 二叉树的最大深度 递归
非递归（队列），层序遍历
BM29 二叉树中和为某一值的路径(一) 递归，有两个终止条件，一个是节点为空，终止；另一个是节点为子节点，而且路径和刚好满足要求。
两个条件分别对应返回值false和true。本级任务是向左右子树递归且把sum值减去当前节点值
BM30 二叉搜索树与双向链表 二叉搜索树的中序遍历，即为顺序链表，所以只需要在中序遍历的过程中建立新的左右指针即可
BM31 对称的二叉树 问题：如何才能将递归返回的所有bool值并在一起？，这题需要用两个递归，
分别比较 子树根1的左子节点 == 子树根2的右子节点 && 子树根1的右子节点 == 子树根2的左子节点
BM32 合并二叉树 递归做法
非递归做法（栈）：维护两个栈，分别保存两棵树的指针（同步保存对应的指针）需要回顾
BM33 二叉树的镜像 调换左右子树 回顾一下官方题解，自己写的递归不够规范优雅
BM34 判断是不是二叉搜索树 非递归中序遍历的过程中，增加前后值大小的判断
递归做法，麻烦在于递归返回的处理，递归过程中间返回的false不能被后面的返回值覆盖，需要特别注意
BM35 判断是不是完全二叉树 层序遍历，一开始把条件想复杂了，其实条件很简单，就是如果访问过NULL之后，还有节点没访问，那就不是完全二叉树。情况归纳做的不好
BM36 判断是不是平衡二叉树 需要理解递归的本质，以及技巧（递归、回溯、剪枝、空间换时间）
BM37 二叉搜索树的最近公共祖先 类似于BM7 链表中环的入口结点，根据二叉搜索树的性质分别获得p和q的搜索路径，然后比较两条搜索路径的相同元素
BM40 重建二叉树 根据前序序列和中序序列还原二叉树，利用前序确定下一个元素，利用中序确定左右子树元素，递归
BM39 序列化二叉树 知识点一：string转char（见下例）
知识点二：*int转string
知识点三：char转int
知识点四：C++指针
前序遍历（递归）
BM41 输出二叉树的右视图 我的做法：前序+中序，重建二叉树；层序遍历二叉树，每层的最后一个节点加入结果数组
  • recursion，递归
  • traverse，穿过
1
2
3
4
5
6
7
8
9
10
11
12
13
//string转char*
string res;
char* charRes = new char[res.length()+1];
strcpy(charRes,res.c_str());
charRes[res.length()]='\0';

//int转string
int x = 12;
strring temp = to_string(x);

//char转int
char c=2;
int val = c-'0';

四、栈、队列、堆

题目 描述
BM45 滑动窗口的最大值 知识点一：双端队列（实现单调队列）
知识点二：双指针
BM46 最小的K个数 解法一：堆（优先队列）
解法二：排序
解法三：快排改编（快排很不熟悉）
BM47 寻找第K大 依然卡在快排上
BM48 数据流中的中位数 做法一：插入排序，C++自带的lower_bound()函数和vector的insert函数
做法二：维护两个堆（最大堆和最小堆）
BM49 表达式求值 算术优先级的处理

算术运算符的优先数

操作服op # ( *,/,% +.- )
isp（栈内优先数） 0 1 5 3 6
icp（栈外优先数） 0 6 4 2 1

处理方式：

1
2
3
4
5
6
7
字符表达式后面加#，Ops栈底放#，Nums栈放数字
while(Ops栈不空)
    数字，入栈
    icp(ch) > isp(op) ch进栈，读入下一个字符
    icp(ch) < isp(op) op退栈，num退栈两次，获得两个数，计算，结果入栈
    icp(ch) == isp(op) op退栈，如果是'('就读入下一个字符
return Nums.top()

最大堆、最小堆的定义方式：

1
2
priority_queue <int,vector<int>,greater<int> > q;	//最小顶堆
priority_queue <int,vector<int>,less<int> >q;		//最大顶堆

二分查找函数：

1
2
3
4
5
lower_bound(起始指针，终止指针，查找值)	//返回大于或等于目标值的第一个位置
upper_bound()	//返回大于目标值的第一个位置
binary_search()	//若目标值存在则返回true，否则返回false
    
iterator insert(pos,elem)	//在迭代器 pos 指定的位置之前插入一个新元素elem，并返回表示新插入元素位置的迭代器。

快排的多种做法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
void QuickSort(vector<int> &A,int L,int R){
    if(L<R){
        int mid = partition(A,L,R);	//分割左右区间
        QuickSort(A,L,mid);			//采取右边界不能访问，即左开右闭的区间 [L,R)
        QuickSort(A,mid+1,R);
    }
}

//众多方法的区别就体现在如何划分左右区间上面
int partition(vector<int> &A,int L,int R){	//版本一，对向双指针
    int pivot = A[L];		//支点的选择也有很多策略，复杂情况下选择居中的元素时间效率更高
    int left=L,right=R-1;	//这里R是边界值，不可取
    while(left < right){
        while(left<right && A[right]>=pivot){right--;}
        A[left] = A[right];
        while(left<right && A[left]<=pivot){left++;}
        A[right] = A[left];
    }
    A[left] = pivot;		//while结束后，left==right，所以这里取left和right都一样
    return left;
}

int partition(vector<int> &A,int L,int R){	//版本二，同向双指针
    int pivot = A[L];
    int i=L;
    for(int j=L+1;j<R;j++){
        if(A[j]<pivot){
            swap(A[i++],A[j]);
        }
    }
    return i;
}

int partition(vector<int> &A,int L,int R){	//版本三，选择居中支点
    int t = (L+R)/2;
    int pivot = A[t];
    swap(A[L],A[t]);
    
    //后面的步骤一样
    int left=L,right=R-1;	//这里R是边界值，不可取
    while(left < right){
        while(left<right && A[right]>=pivot){right--;}
        A[left] = A[right];
        while(left<right && A[left]<=pivot){left++;}
        A[right] = A[left];
    }
    A[left] = pivot;		//while结束后，left==right，所以这里取left和right都一样
    return left;
}

五、哈希

题目 描述
BM50 两数之和 遍历数组，判断（目标值 - 当前值）是否在哈希表中，不在则将当前值和下标加入哈希表。unordered_map
BM51 数组中出现次数超过一半的数字 做法一：哈希表统计出现次数，两次遍历
做法二：候选法（最优解），借助cand候选值和count计数器模拟出两两不同相消的操作（巧妙）
BM52 数组中只出现一次的两个数字 做法一：哈希表统计
做法二：异或运算（需要熟悉异或运算的性质）
BM53 缺失的第一个正整数 做法一：unordered_set，插入用emplace（效率比insert高），查找用find
做法二：原地哈希，借用数组的下标作为哈希键
BM54 三数之和 找a+b+c=0的组合，排序+（固定单点+双指针）遍历，注意点细节很多（数组为空，元素重复）

异或运算的性质：

1
2
3
a⊕b⊕c⊕b⊕c=a
0⊕0=0
0⊕1=1

六、递归/回溯

题目 描述
BM55 没有重复项数字的全排列 传统做法，访问标记数组+临时存放数组空间
题解做法：递归swap两两交换位置（关键要能够图解过程）
BM56 有重复项数字的全排列 传统做法 + 去重操作：（如果当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用，也不需要将其纳入，前提：元素有序）
i>0 && initStr[i-1]==initStr[i] && !vis[i-1]
BM57 岛屿数量 深度优先搜索，我的做法：借助标记数组（开辟一个辅助数组）
题解做法：深度优先搜索的时候将1修改为0，缺点：改变了原数组
BM58 字符串的排列 字符可能重复，与BM56类似，BM56与这里的区别在于BM56是有序序列，而这里的字符串是无序的
做法一：是先将字符串排序，然后在排列的过程中避免重复项（与BM56的做法一致）
做法二：递归swap两两交换位置，利用set去重，最后set转vector返回
BM59 N皇后问题 递归层数 作为行数（直接满足不同行的条件）；
递归内部循环遍历每个可能都列号，判断是否满足不同列、不在同一斜线的条件
难点在于同一斜线的判断：这里有两种方法：
方法一：row-col 可以唯一确定正斜线，row+col可以唯一确定反斜线
方法二：当前点（row,col）与之前的所有点（i,j）遍历比较，abs(row-i) == abs(col-j)可以判定处于同一斜线
可以采用标记集合set（方法一，空间换时间，递归+回溯），也可以写一个判定函数遍历所有点一一比较
BM60 括号生成 与BM56类似，初始化一个有序的括号序列，然后按照BM56的思路进行全排列，
在排列的过程中对括号进行有效性监视，我在这里采用的方法是借助一个变量记录当前括号序列的累加值
遇到左括号，加一；遇到右括号，减一；递归过程如果累加值小于0，说明有多余的）在（前面，
跳过当前的序列
官方题解的解释：保证左括号出现的次数比右括号多时我们再使用右括号就一定能保证括号合法了
BM61 矩阵最长递增路径 与BM57类似，都是对二维矩阵进行递归深度优先搜索，使用标记数组记录递归过程访问过的节点
题解做法：使用dp数组，记录每个节点出发的最长路径（动态规划、空间换时间，可以避免重复的递归）

递归全排列两种做法：

  • 传统做法：访问标记数组+临时存放数组空间，适用于各种类型的容器，包括原始的数组int A[]
  • swap做法：递归swap两两交换位置，适用于现成的容器具有现成的swap等方法可以直接调用

递归过程图解：

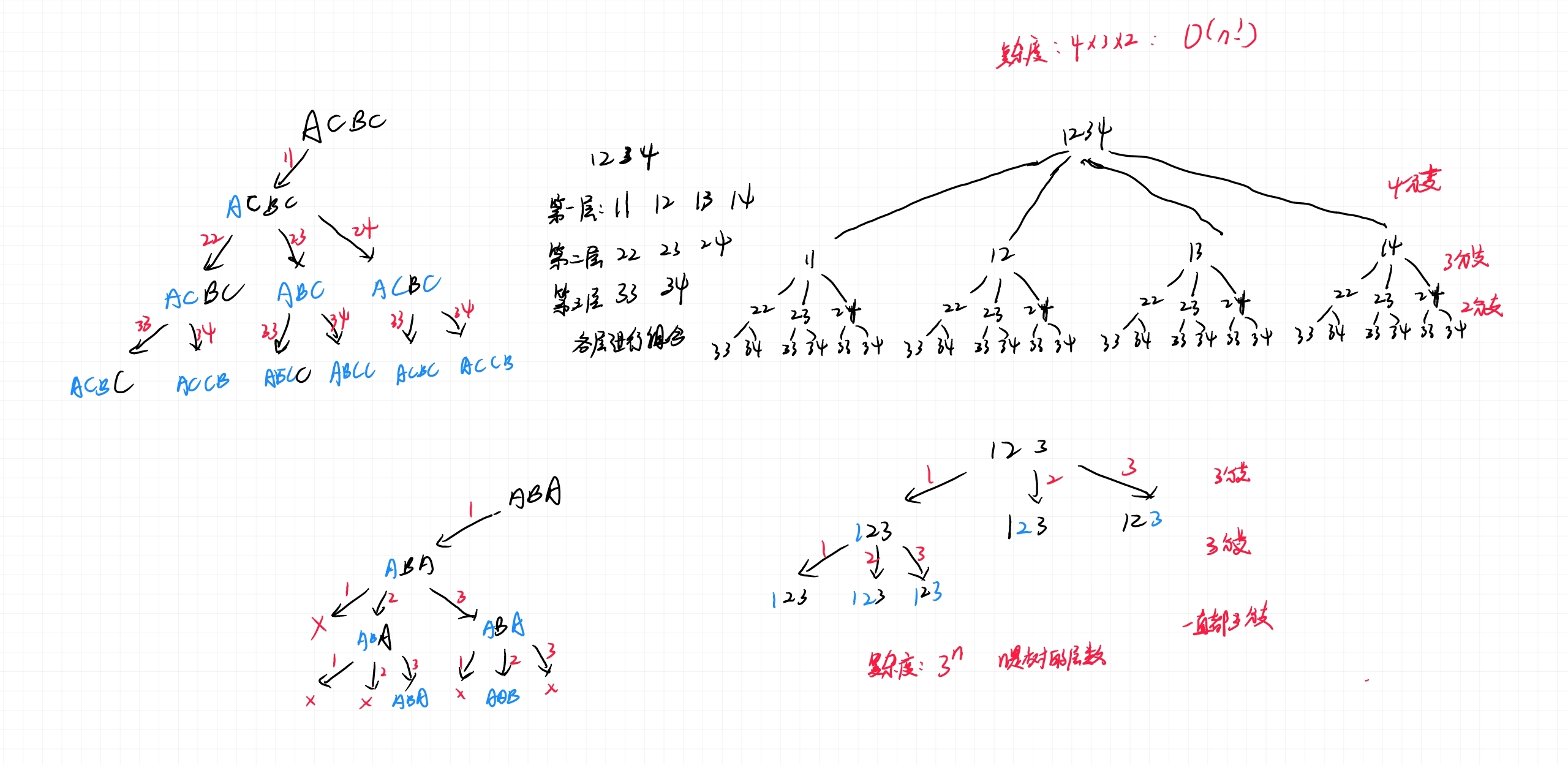
微信图片_20220519111009

七、动态规划

题目 描述
BM62 斐波那契数列 做法一：递归+记忆化搜索
做法二：动态规划（迭代）
BM63 跳台阶 BM62的变形
A[i] = A[i-2] + A[i-1]
BM64 最小花费爬楼梯 动态规划：将问题的解决方案视作一系列决策的结果
过程为：确定初始状态，然后执行状态转移。
A[i] = min (A[i-2]+cost[i-2] , A[i-1]+cost[i-1])
BM65 最长公共子序列(二) dp矩阵记录最长长度，dir矩阵记录每个点来自的方向
状态转移方式：
如果str1[i-1] == str2[j-1] ，那么dp[i] [j]=dp[i-1] [j-1] +1
否则，dp[i] [j]= max(dp[i-1] [j] , dp[i] [j-1] )
BM66 最长公共子串 与BM65类似，维护dp的方式稍有不同
如果str1[i-1] != str2[j-1] ， 那么 dp[i] [j] =0
因为子串要求必须相邻
BM67 不同路径的数目(一) F[i] [j] = F[i-1] [j] + F[i] [j-1]，左、上边界外层填充0
BM68 矩阵的最小路径和 左、上边界外层填充极大值 INT_MAX
初始化dp[1] [1] = matrix[0] [0]
后续：dp[i] [j] = min(dp[i-1] [j], dp[i] [j-1]) + matrix[i-1] [j-1]
BM69 把数字翻译成字符串 一维的dp数组，巧妙的地方，增加了一个值为1的前哨
与BM62、BM63相同的本质，区别在于这里增加了一定的条件
BM70 兑换零钱(一) 动态规划的状态转移方式是从后往前推导出来的，但是计算却是从前往后计算，它需要一个初始状态。
两种做法，做法一：暴力枚举+记忆化搜索，好处：修改一下可以获取所有符合条件的组合
做法二：动态规划，dp数组初始化为极大值，dp[0] = 0;
状态转移方程：dp[i] = min( dp[i], dp[i-arr[j]]+1)
判断是否货币组合是否恰好满足条件：看dp[aim]是否大于aim（大于，就说明dp[aim]没有改变过，没有合适的组合）
BM71 最长上升子序列(一) 将问题拆分成一个个子问题，将序列从长度1一直拆分到完整长度，依次获得每个长度子序列的最长上升子序列
双重循环，第一重循环遍历序列的每个长度的子序列，从1到length
第二重循环，判断当前子序列最长的上升子序列长度
第一重：for(int i=0;i<arr.length();i++) 第二重：for(int j=0;j<i;j++)
判断：if(arr[i]>arr[j] && dp[j]+1>dp[i]) dp[i] = dp[j]+1
BM72 连续子数组的最大和 动态规划，初始化：dp[0] = arr[0]
状态转移方程： dp[i] = max( arr[i] , arr[i]+dp[i-1])，
因为数组内存在负数，所以并不是元素越多越好
解释：如果当前值加上前面子序列的子数组最大和比原来小，那么对于以当前值为结尾的子序列，当前值就是连续子数组的最大和
如果当前值加上前面子序列的子数组最大和比原来大，那么就应该把当前值加入到最大和子数组中，形成新的最大和子数组
BM73 最长回文子串 回文子串的判定：从中间向两边扩展，左右相同就是回文子串（注意：“中间”包含一个字符和
两个字符两种情况，即奇数回文子串和偶数回文子串两种情况）
遍历字符串的每个字符，分别以每个字符和每两个字符为中心，向两边扩展求回文子串的长度
取遍历过程中最大的长度即为结果
BM74 数字字符串转化成IP地址 string转int：stoi(str) substr(int pos,int length第二个参数不给的话默认截取到尾部)
做法一：递归回溯+剪枝，学会一个string类型回溯的技巧：在改变本级string之前，先保存一遍
回溯的时候直接赋值回这个保存的临时值就OK了，这是string类型独有的回溯技巧（数组不适用）
做法二：迭代枚举
BM75 **编辑距离(一)**（较难） dp[i] [j]表示从两个字符串首部各自到str1[i] 和 str2[j]为止的子串需要的编辑距离
初始条件：假设第一个字符为空，那么字符串一每次增加一个字符，对应dp[0] [j]每次递增一
同理，dp[i] [0]每次递增一
状态转移：如果str1[i]与str2[j]相等，那么dp[i] [j]当前字符不需要改变，等于dp[i-1] [j-1]
如果str1[i]和str2[j]不相等，那么最短距离需要在【修改当前字符、删除当前字符、增加新字符】当中选择一个最小值，即dp[i] [j] = min(dp[i-1] [j-1], min(dp[i-1] [j], dp[i] [j-1])) + 1
难点：在于理解修改、删除、增加分别对应的dp操作
BM76 正则表达式匹配（较难） 还是不太理解状态转移到原理
BM77 最长的括号子串 必须通过元素下标计算有效括号的长度！（具体解释写在了牛客BM66的“讨论”里面了）
BM78 打家劫舍(一) 不能偷相邻2家，那么中间可能会跳过1家，也可能为了偷更多钱跳过2家
dp[1] = nums[0] 只有一家，那么偷它收益最大
dp[i] = max(dp[i-1] , dp[i-2]+nums[i-1])
解释：如果偷当前家，那么累计收益为当前家+上上家的累计最大收益；如果不偷当前家，那么累计收益是截止上家的累计最大收益
BM79 打家劫舍(二) 链型数组变成环型数组，第一家和最后一家不能同时偷。
所以分两种情况：偷第一家不偷最后一家，不遍历最后一个元素。偷最后一家不偷第一家，不遍历第一个元素
BM80 买卖股票的最好时机(一) 题目：一次交易
贪心做法：每日价格-前面最小价格。初始化第一个数为最小值，然后遍历，如果当前值比最小值小，更新最小值；如果当前值比最小值大，比较Max和当前值-最小值的大小，维护Max
BM81 买卖股票的最好时机(二) 题目：不限次数交易
贪心做法：把每段单调增区间的收益加进去
BM82 买卖股票的最好时机(三) 题目：限制两次交易
没做

列举出现过的状态转移方程

  • BM72，单个数组连续子串最大值
1
dp[i] = max(arr[i] , arr[i]+dp[i-1] )
  • BM66，两个数组的最长公共子串
1
2
if(str[i]==str[j]) dp[i][j] = dp[i-1][j-1]+1;
else  dp[i][j]=0;
  • BM65，两个数组的最长公共子序列
1
2
if(str[i]==str[j]) dp[i][j] = dp[i-1][j-1]+1;
else  dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
  • BM71，单个数组的最长上升子序列
1
if(arr[i]>arr[j] && dp[j]+1>dp[i]) dp[i]=dp[j]+1;

八、字符串

题目 描述
BM83 字符串变形 方法一：分割字符串+栈
方法二：双反转（先反转整个字符串，再单独反转单词）
BM84 最长公共前缀 substr(pos,length)
BM85 验证IP地址 IPv4的条件：1.数值方面，数字字符只能在0-9范围、不能有前导0、数值小于等于255、数值个数为4；2.符号方面，点号的个数为3
IPv6的条件：1.数值方面，数字字符在0-9或者A-Z或者a-z的范围、数值字符个数小于等于4、数值个数为8；2.符号方面，冒号的个数为7
BM86 大数加法 扩展
知识点一：int转string
知识点二：string转int：stoi(string)
知识点三：char与int互转
知识点四：char*与string互转
  • string转int
1
2
3
4
5
6
7
#include<string>
using namespace std;

string str="123";
int value = stoi(str);
int result = value + 27;
cout<<result;	//150
  • int转string
1
2
3
4
5
6
7
#include<string>
using namespace std;

int value = 123;
string str = "456";
str += to_string(value);
cout << str;	//456123
  • char和int互转
1
2
3
4
5
6
7
8
9
10
11
/*char转int*/
char ch = '3';
int value = ch-'0';	
cout<< value +1;	//4，如果不-'0'，结果是52，因为3对应的ascii码是50

/*int转char（备注：int只能是个位数，不然就不能转char类型了）*/
int value = 2;
char ch = value + '0';
string str="1";
str+=ch;
cout<<str;		//12，如果不转char（不+'0'），结果为1，因为ascii值2对应的是一个不显示的字符
  • string转char*，使用c_str()方法
1
2
3
4
5
6
7
#include<string>
using namespace std;

char c[20];			//初始化一个char数组空间
string str = "12345";
strcpy_s(c, str.c_str());
cout << c;		//12345
  • char*转string，直接赋值即可
1
2
3
const char* p = "hello";
string str = p;	//声明和定义不一定需要在一起
cout << str;	//hello

九、双指针

题目 描述
BM87 合并两个有序的数组 逆向思考，因为题目要求将结果放置到原数组中，所以为了不覆盖原数组，可以从预计两个数组合并后的末尾开始放置。
BM88 判断是否为回文字符串 做法一：从两端向中间遍历（对向相迎双指针）
进阶做法：从中间向两遍遍历，长度分奇数和偶数两种情况
BM89 合并区间 在类里面自定义比较函数，需要加上static关键字
BM90 最小覆盖子串 遍历unordered_map的方法，前后双指针，用map记录覆盖子串的情况
用一个函数判断是否覆盖完子串，没有覆盖完，前指针移动扩大窗口范围；覆盖完之后，后指针移动缩小窗口。用另外的left和right记录最小窗口
BM91 反转字符串 太过简单
BM92 最长无重复子数组 与BM89是同一种题型，滑动动态大小窗口，
BM89的特点是：要求覆盖子串，所以需要子串中所有元素都至少出现一次，可以多次，所以适合用map统计频数
而这题的特点是：要求不重复，所以子串中的元素出现次数只能少于一次，适合用set判断是否出现过（用map时间复杂度就高了）
BM89求最小，所以初始值L和R要取尽可能大。这题求最长，所以初始值L和R要尽可能小
两题相同的地方是滑动窗口的过程，不同点在于滑动过程中的比较，BM89是滑动寻找满足条件的情况，这里是滑动到不满足条件为止。L和R都是在满足条件的情况下取的最值
BM93 盛水最多的容器 贪心+双指针，贪心利用了“短板效应”，水桶高度取决于短的那条边，所以每次舍弃短板，寻找更长的板（不一定能找到）
BM94 接雨水问题 做法一：双指针，利用短板效应，最简单容易理解
做法二：动态规划，计算出中间每个柱子的两侧最大高度，取最小的那个就是盛水高度
做法三：单调栈，依次计算每个V字形区间的盛水量，较麻烦

遍历unordered_map的方法 :

1
2
3
4
for (auto iter = hash.begin(); iter != hash.end(); iter++){
    cout<<iter->first<<" "<<iter->second<<endl;
}
//可以直接用方括号的方式直接赋值，或者修改值

十、贪心算法

题目 描述
BM95 分糖果问题 使用辅助数组记录结果，从左往右遍历，增区间从1开始递增；
从右往左遍历，增区间从1开始递增，稍微不同的是这时还需要比较A的值，
增区间如果左边糖果已经比右边多了那么不用改变，因为这是从左往右遍历的结果；
但如果增区间左边仍然比右边少，那么需要比右边多加一
贪心体现在：从左往右、从右往左遍历的时候都从最小的1开始递增
BM96 主持人调度（二） 本题要求：活动时间有重合，主持所有活动需要多少名主持人
做法：step1，将数组按start时间排序；step2，使用辅助数组A，模拟主持人阵容；step3，遍历arr数组，将每场活动的end时间加入到A数组，如果A中有元素的end时间小于等于当前活动的start时间，那么加入到当前A元素；如果当前A中没有元素的end时间小于等于当前活动的start时间，需要新增加一个空间（增加一名主持人）；step4，最后统计A的大小
题目扩展：活动时间有重合，一个主持人最多能主持多少场活动
做法：将arr数组按end时间排序，依次遍历arr，如果当前start大于等于上一个end，结果+1，同时end更新为当前活动的end

十一、模拟

题目 描述
BM97 旋转数组 三次翻转，reverse(start,end)、reverse(start,start+m)、reverse(start+m,end)
BM98 螺旋矩阵 一开始用while，自己给自己找麻烦
分别使用left、right、top、bottom记录四个边界
所有操作可以分为4步：第1步，上边界从左到右，做完上边界下移；
第2步，右边界从上到下，做完右边界左移；
第3步，下边界从右到左，做完下边界上移；
第4步，左边界从下到上，做完左边界右移。
其中每一步做完之后，检查对应边界的情况，比如右边界左移之后，检查左边界是否超过了右边界（重合不算）
BM99 顺时针旋转矩阵 顺时针旋转：[i] [j] = [n-1-j] [i]
180度旋转：[i] [j] = [n-1-i] [n-1-j]
逆时针旋转： [i] [j] = [j] [n-1-i]
倒置转换：先将上三角矩阵和下三角矩阵转置，然后每行倒置，利用矩阵变换的规律
BM100 设计LRU缓存结构 最久未用先删除策略，使用计数器记录每个key距离上次被使用的时间，最长时间没被使用的删除
BM101 设计LFU缓存结构 最少使用最早调用先删除策略
做法：使用计数器记录key被调用的次数，使用计时器记录每个key距离上一次调用的时间
细节：不管是set还是get操作，每一次调用都要让所有key的计时器加一，因为没有注意到这个细节导致了出错
算法与数据结构
#算法
算法题练习笔记
http://timegogo.top/2022/05/27/算法与数据结构/牛客算法刷题记录/
作者
丘智聪
发布于
2022年5月27日
更新于
2023年7月16日
许可协议