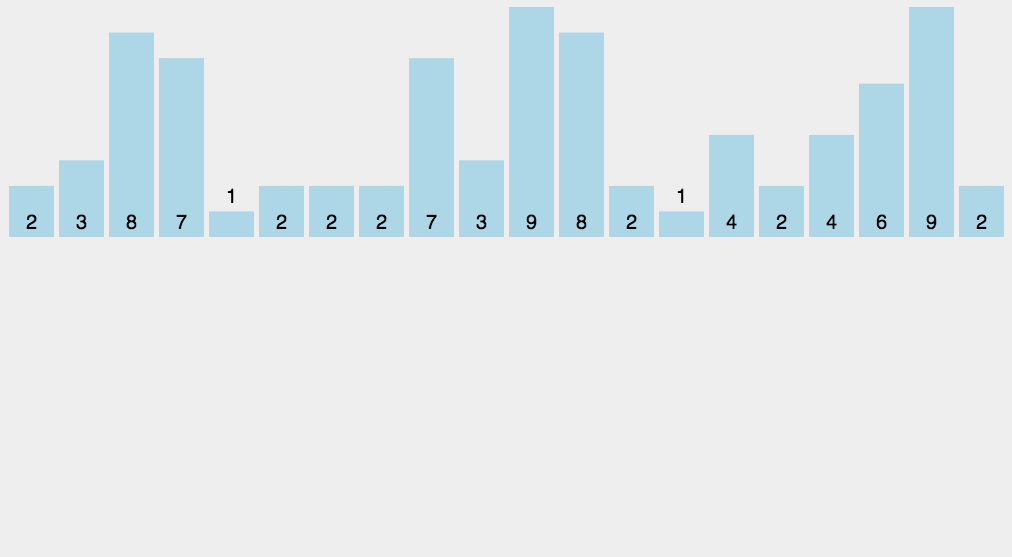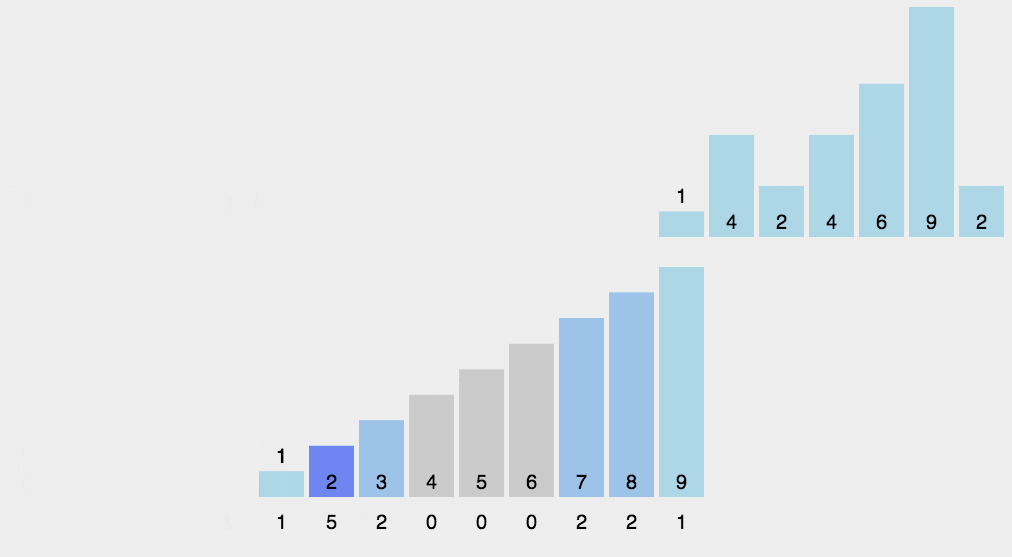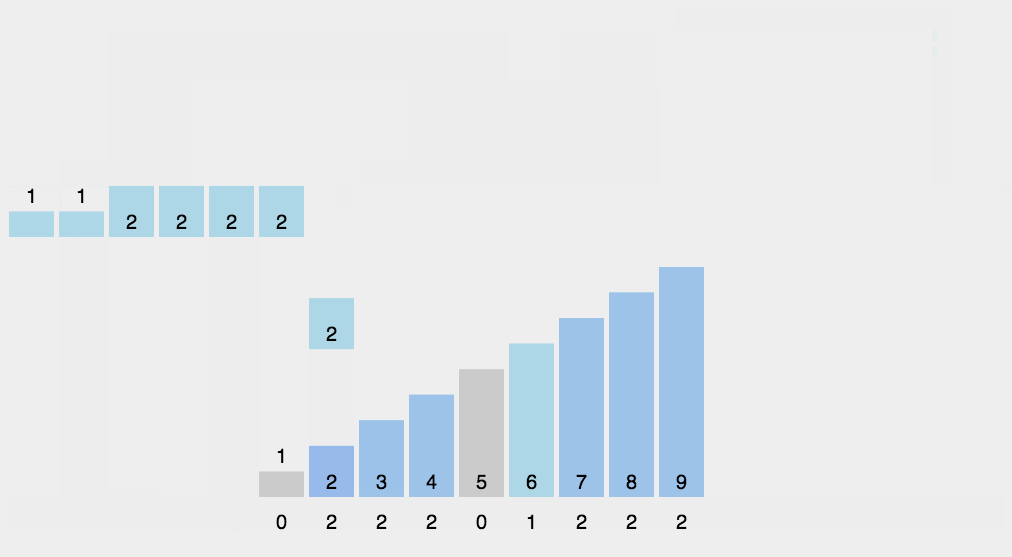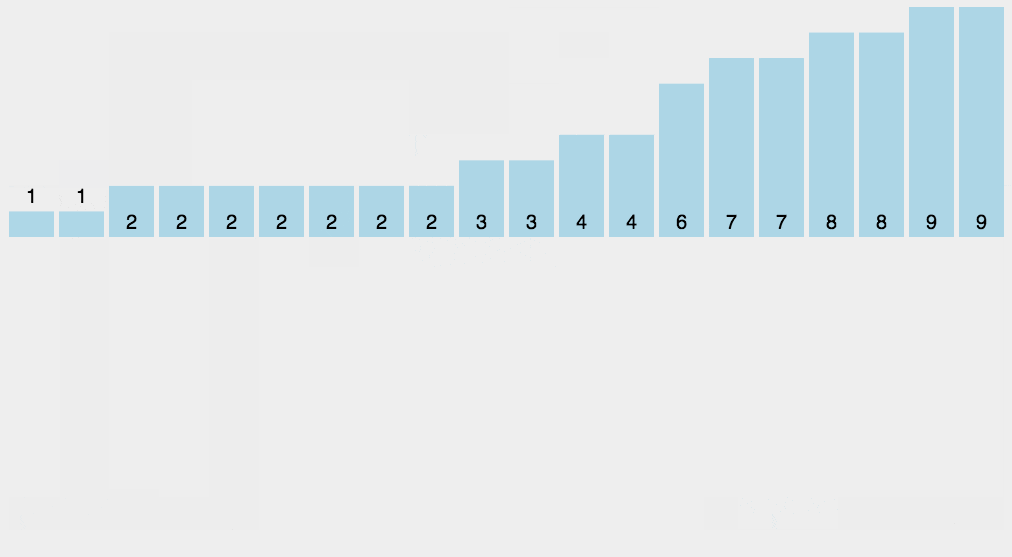各种排序算法的思想和实现，如：快速排序、归并排序等

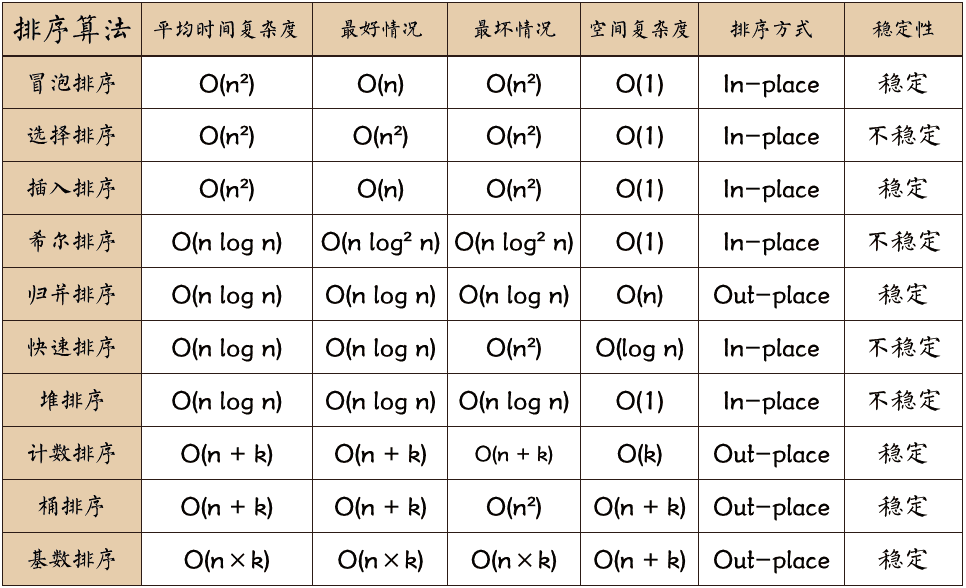
排序算法汇总

一、快速排序

分治思想：挖坑填数+分治法

void quick_sort(vector<int>& arr, int L, int R) {
	if (L < R) {
		int i = L, j = R;
		int pivot = arr[L];
		while (i < j) {
			while (i < j && arr[j] >= pivot)j--;
			if (i < j) {
				arr[i] = arr[j];
				i++;
			}
			while (i < j && arr[i] < pivot)i++;
			if (i < j) {
				arr[j] = arr[i];
				j--;
			}
		}
		arr[i] = pivot;		//此时应该是i==j，所以用i和用j其实是一样的
		quick_sort(arr, L, i-1);
		quick_sort(arr, i + 1, R);
	}
}

参考：快速排序 | 菜鸟教程 (runoob.com)

二、归并排序

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4. 重复步骤 3 直到某一指针达到序列尾；
5. 将另一序列剩下的所有元素直接复制到合并序列尾。

void mergesort(vector<int>& arr, int start, int end) {
	if (start < end) {
		int mid = (start + end) / 2;
		mergesort(arr, start, mid);
		mergesort(arr, mid + 1, end);
		merge(arr, start, mid, end);
	}
}
void merge(vector<int>& arr, int start, int mid, int end) {
	//将左右区间的子数组 拷贝一份，然后就可以直接在原数组进行修改
	vector<int> Left(arr.begin() + start, arr.begin() + mid + 1);
	vector<int> Right(arr.begin() + mid + 1, arr.begin() + end + 1);
	int L = 0, R = 0;			//子数组（备份）的下标索引
	Left.push_back(INT_MAX);	//操作上的技巧，在子数组最后一位加入MAX值，这样就可以确保另外一个子数组的所有剩余元素
	Right.push_back(INT_MAX);	//在循环中，全部被放入。而不用另外去处理剩余的子数组元素

	for (int i = start; i <= end; i++) {
		if (Left[L] <= Right[R]) {
			arr[i] = Left[L];
			L++;
		}
		else {
			arr[i] = Right[R];
			R++;
		}
	}
}

三、冒泡排序

重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。这个算法的名字由来是因为越小的元素会经由交换慢慢”浮”到数列的顶端。

void bubble_sort(vector<int>& arr){
    int len = arr.size();
    for(int i=0;i<len-1;i++){
        for(int j=0;j<len-1-i;j++){
            if(arr[j]>arr[j+1]){
                swap(arr[j],arr[j+1]);	//swap是std的函数，添加了using namespce std即可用
            }
        }
    }
}

四、选择排序

选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

void select_sort(vector<int>& arr){
    int len = arr.size();
    for(int i=0;i<len;i++){
        int min = i
        for(int j = i+1;j<len;j++){
            if(arr[j]<arr[min]){
                min = j
            }
        }
        swap(arr[i],arr[min]);
    }
}

五、插入排序

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

void insertion_sort(vector<int> &arr){
    for(int i=1;i<arr.size();i++){
        int key = arr[i];
        int j = i-1;
        while(j>=0 && arr[j]>key){
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = key;
    }
}

优化途径：对有序序列的线性遍历，改为二分遍历

六、堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法，可以分为大顶堆（用于升序排列）、小顶堆（降序排列）

堆的性质：子结点的键值或索引总是小于（或者大于）它的父节点

步骤：

• 将数组转换成堆，将数组元素依次插入堆，形成一个初始的堆
• 把堆头和堆尾互换，然后堆的长度减一，并使用shift_down()方法把新的堆头调整到正确的位置
• 重复上一步，直到堆的长度为1，此时数组已经拍好序

建立堆，根据现有数组，建立堆结构，调用shiftDown算法，从（树的最底层）最后一个父节点开始，依次往上（往前）调用shiftDown，让父节点放置到对应的位置（要满足子节点的值总是小于（或者大于）它的父节点）

向堆插入元素，首先将元素插入堆（也就是数组）末尾，然后调用shiftUp方法，将新元素放到相应位置

shiftDown方法中，有一个步是要比较左右子节点的大小。

• 如果是大顶堆，就要将父节点与左右子节点较大的一个比较；
• 如果是小顶堆，就要将父节点与左右子节点中较小的一个比较

七、基数排序

原理和过程看图，从低位（个位）开始比较

八、计数排序

适用于范围给定（从n-m），且范围不大的数组排序，原理如下：